24/06/2025
Blog technique
La cryptographie post-quantique dans TLS (2/2) – Les signatures et le chiffrement du flux de données
Lucile RAZE, équipe CESTI
TLS est un protocole permettant d’assurer la confidentialité et l’intégrité des échanges entre un client et un serveur et à minima l’authenticité du serveur. Dernièrement, la cryptographie post-quantique (abrégée PQC) y a été intégrée.
Un premier billet a traité en détails l’échange de clé. Ce nouveau billet a pour sujet le reste de la cryptographie dans TLS, soit le chiffrement du flux de données et les signatures.
Le chiffrement du flux de données
Le blog précédent a mis en évidence les différences entre les suites de chiffrement dans TLS 1.2 et TLS 1.3. En résumé, dans TLS 1.3, les algorithmes responsables de l’échange de clés et de l’authentification ne sont pas inclus dans la ciphersuite mais sont spécifiés dans des extensions.
La cryptologie symétrique est, comme l’échange de clé, sensible aux attaques de types Store New Decrypt Later. Il est donc primordial de se protéger dès aujourd’hui de la menace quantique. Contrairement à la cryptographie asymétrique, il n’est pas nécessaire de créer de nouveaux algorithmes résistants à la menace quantique ; il suffit d’augmenter la taille des clés pour le chiffrement et la taille des empreintes pour les fonctions de hachage pour que les algorithmes actuels deviennent résistants. Comme il n’y a pas de nouveaux algorithmes à utiliser, il n’est donc pas nécessaire d’intégrer d’hybridation lors du chiffrement des données.
Pour être robuste face à un ordinateur quantique, la clé d’AES doit donc être d’au moins 256 bits et l’empreinte issue d’une fonction de hachage doit être d’au moins 384 bits.
Dans TLS 1.2, il n’est pas possible de réaliser un échange de clé post-quantique : cela a donc peu d’intérêt de protéger le chiffrement du flux face à un attaquant quantique . En effet, un attaquant quantique pourrait être en mesure de casser l’échange de clés grâce à l’algorithme de Shor pour retrouver la clé de session, et donc pourra déchiffrer le flux (même s’il est chiffré en AES-256).
Dans TLS 1.3, des échanges de clés utilisant ML-KEM sont possibles. Ainsi, il est possible d’utiliser l’une des cinq suites de chiffrement suivantes qui sont proposées :
- TLS_AES_256_GCM_SHA384 ;
- TLS_CHACHA20_POLY1305_SHA256 ;
- TLS_AES_128_GCM_SHA256 ;
- TLS_AES_128_CCM_8_SHA256 ;
- TLS_AES_128_CCM_SHA256.
À ce jour, dans TLS 1.3, seule TLS_AES_256_GCM_SHA384 est robuste dans un contexte post-quantique. Les quatre autres suites ont, à l’algorithme de Grover, une sécurité insuffisante pour la protection de données à long terme.
En synthèse, pour mettre en place un chiffrement TLS robuste à la menace post-quantique, il est nécessaire d’utiliser TLS 1.3 et la suite de chiffrement TLS_AES_256_GCM_SHA384 (avec l’échange de clés équivalent et suffisant)
Les signatures de messages et de certificats
Les signatures ont pour objectif de garantir l’intégrité et l’authenticité de données. Elles sont utilisées à deux étapes du protocole :
- Lors de la vérification de l’intégrité de la chaine de certificats dans le message Certificate ;
- À l’authentification du serveur dans le message Certificate Verify.
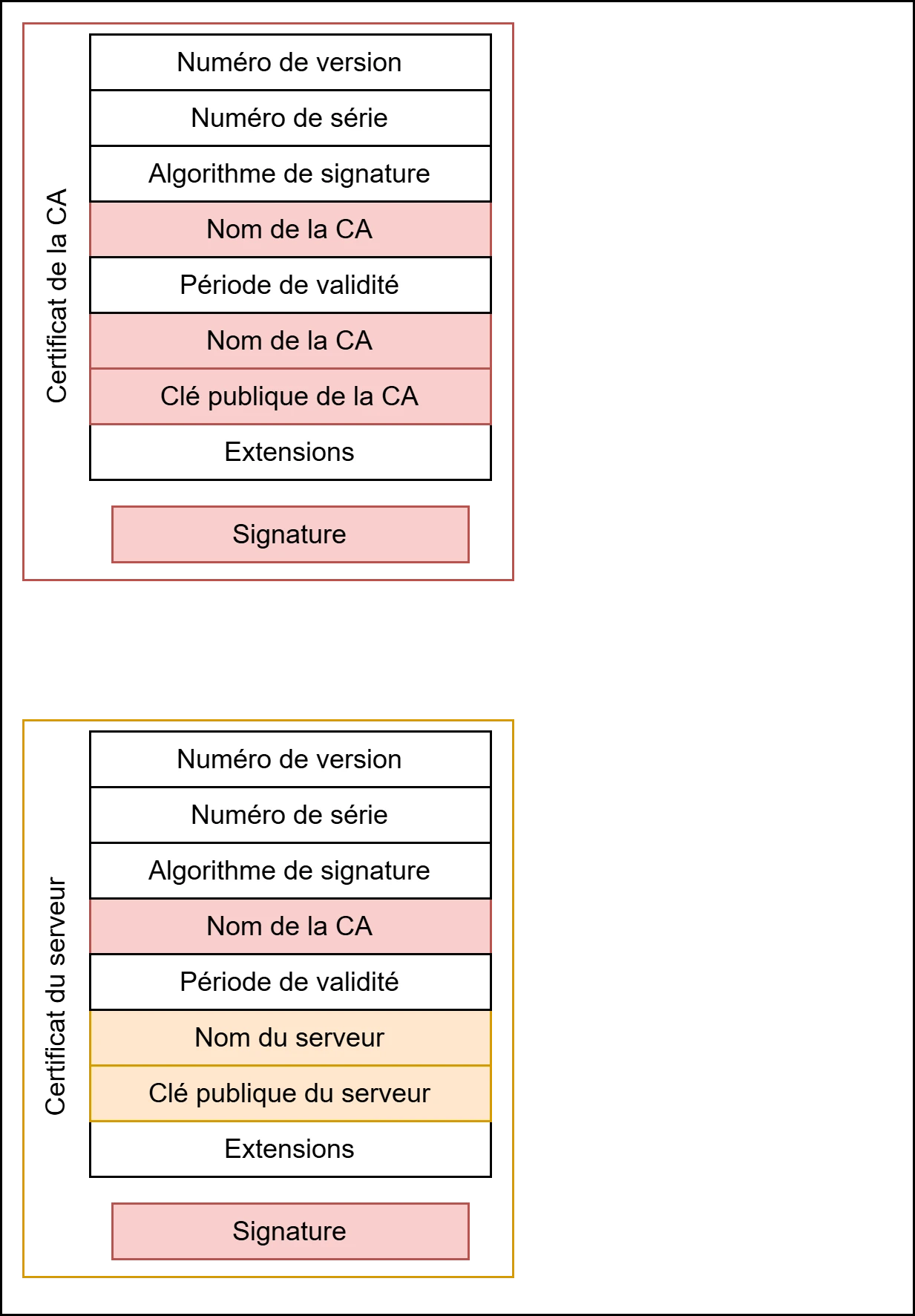
Fonctionnement du message Certificate
Après avoir envoyé son ServerHello et les extensions qu’il souhaite utiliser, le serveur transmet son certificat au client. Lorsque le client reçoit le certificat, il vérifie la cohérence des données ainsi que la validité de la signature du certificat grâce à la clé publique du signataire.
Le client peut également envoyer son certificat pour une authentification mutuelle.
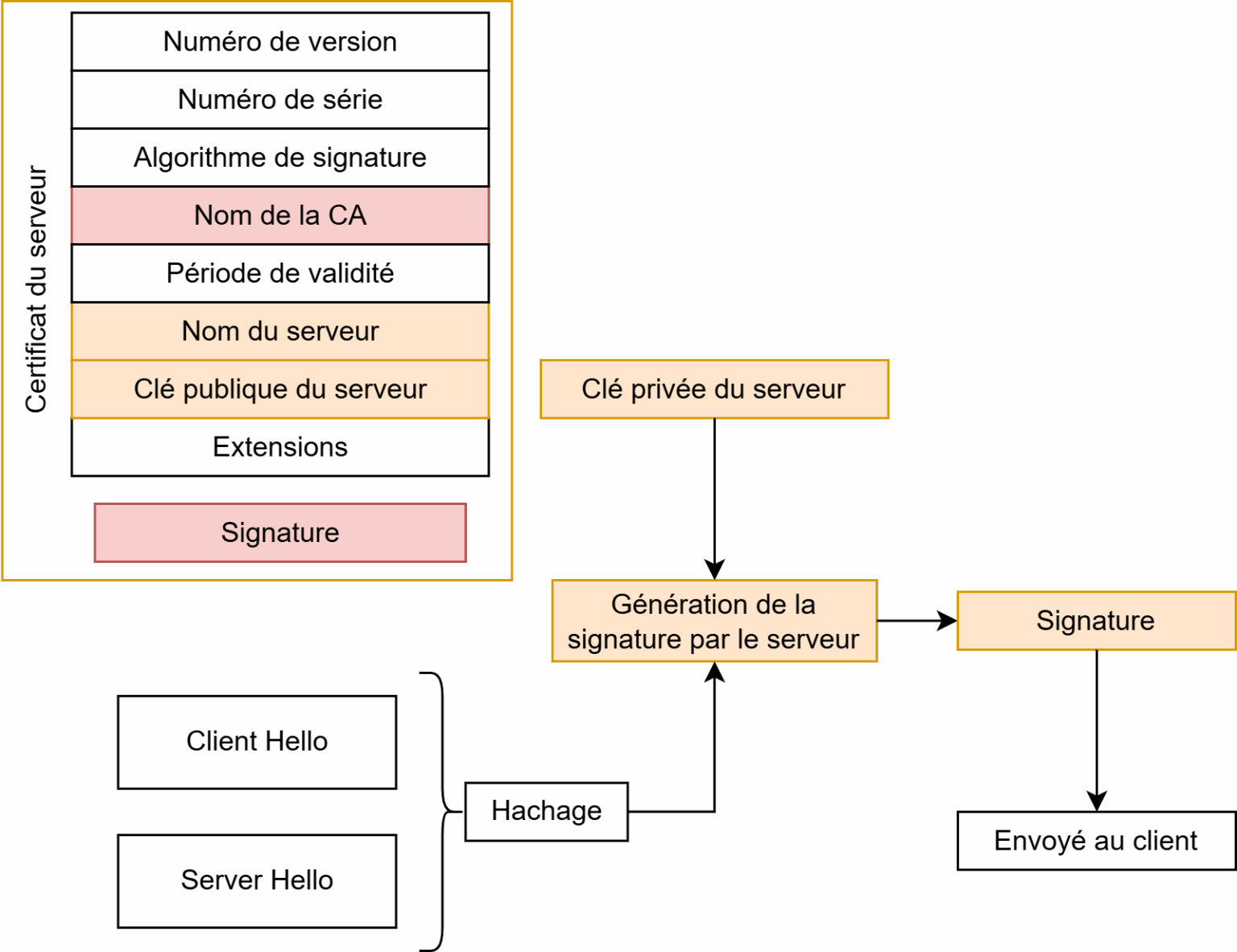
Fonctionnement du message CertificateVerify
Ce message, envoyé par le serveur, a pour objectif de prouver au client qu’il connait bien la clé privée associée à son certificat. Pour cela, le serveur signe un haché des messages de négociation avec sa clé privée. Le client vérifie la signature avec la clé publique contenu dans le certificat.
L’attaque par falsification
Les attaques sur les signatures ont pour objectif de falsifier une signature interceptée, ou le message signé. Ces attaques sont donc des attaques en temps réel et non en différé, ce qui les exclues des attaques du type Store Now Decrypt Later.
Ainsi, et bien qu’il soit important de commencer la transition vers la cryptographie post-quantique également pour les signatures (notamment car tout changement à grande échelle est lent), la protection offerte par les signatures post-quantiques ne sera utile que si un attaquant quantique existe déjà.
L’extension signature_algorithms
Cette extension de TLS permet au client d’indiquer les algorithmes de signatures supportés. Traditionnellement, différentes versions de RSA ou ECDSA y sont mentionnées, par exemple ecdsa_secp256r1_sha256.
Il est maintenant possible d’y indiquer un algorithme de signature post-quantique comme ML-DSA. Un premier draft de RFC sur l’intégration de ML-DSA dans TLS a été publié en mai 2025 : https://datatracker.ietf.org/doc/draft-ietf-tls-mldsa/00/.
Voici un tableau récapitulatif de l’ensemble des valeurs fixées par l’IANA pour les signatures post-quantique, ainsi que les tailles en octets pour chacune des données.
L’ANSSI recommande d’utiliser seulement les mécanismes dont le niveau de sécurité est au moins équivalent à celui d’AES-192 ; c’est pourquoi ML-DSA-44 n’est pas recommandé.
De plus, l’ANSSI recommande d’utiliser l’hybridation de deux algorithmes de signatures (un classique et un post-quantique) durant la phase de transition vers la cryptographie post-quantique, au lieu d’utiliser uniquement des algorithmes PQC. Néanmoins, à ce jour, aucune signature hybride n’est proposée par l’IANA.
À noter, des discussions sur la façon de créer un certificat contenant une double signature, une classique et une post-quantique, sont en cours pour standardiser un format, mais cela n’est pas encore mis en œuvre dans TLS.
En synthèse, pour mettre en place un chiffrement TLS robuste à la menace post-quantique, il est nécessaire d’utiliser TLS 1.3 et l’algorithme de signature ML-DSA-65 ou ML-DSA-87. Actuellement l’hybridation des signatures n’est pas proposée dans TLS, mais des réflexions à ce sujet sont en cours.
En conclusion
Il est donc possible d’obtenir une configuration TLS permettant de se protéger entièrement de la menace quantique, autant durant l’échange de clé, l’authentification ou le chiffrement du flux !
À noter que la version 3.5.0 de la bibliothèque OpenSSL supporte les différentes versions de ML-KEM et ML-DSA.









