CRY.ME: Private key recovery with a single signature

31/01/2024

Blog technique

CRY.ME: Private key recovery with a single signature

Team CESTI

Amossys is one the few ITSEFs in France (called CESTI in French) licensed by the ANSSI and accredited by COFRAC [accreditation no 1-2190, scope available at www.cofrac.fr]. We evaluate security products with a rigourous methodology, which can result in a visa de sécurité delivered by the ANSSI.

On a regular basis, the ANSSI challenges the ITSEFs on their skills.
In 2022, they collaborated with CryptoExperts to develop a secure
messaging application called CRY.ME (Cryptographic Messaging) and based
on the Matrix protocol to evaluate our cryptographic
skills.

Then, in June 2023, the ANSSI and CryptoExperts publicly released the source code and all elements needed to run the application, with the documentation that was originally provided to us (see the SSTIC 2023 presentation), so it can be used for pedagogic purposes: https://github.com/anssi-fr/cry-me

Many vulnerabilities were included to test our abilities to find them and, if possible, to exploit them. In this article, we explore one vulnerability that we found during the original challenge, and explain how we exploited it: can we find a secret key from a single signature?

Schnorr signature

The messaging application uses many cryptographic mechanisms and protocols (those are described in the cryptographic specifications). We focus on the signature algorithm which is based on the Schnorr algorithm and an elliptic curve. Its code can be found in the file ecc_signature.c.

The Shnorr signature is very close to the ECDSA signature. The signature generation is given below (it is not needed to know about elliptic curve calculation in this article, so it is not important to focus on it):

To sign a message $M$ with a private key $\alpha$ :

Generate a random nonce $k$ ;
Compute the scalar multiplication $Q = [k]G$ where $G$ is the base point of the elliptic curve;
Compute the value $r = H(Q_x, Q_y, M)$ where $H$ is a hash function (such as SHA-256, the inputs are concatenated) and $r$ is interpreted as an integer;
Use the private key $\alpha$ to compute $s = k + \alpha r \bmod n$ where $n$ is a parameter of the elliptic curve (the number of points);
The signature is the couple $(r, s)$ , except in the very improbable case that $r \bmod n$ or $s$ is zero in which case the procedure needs to be repeated.

The important thing to retain is the equation $s = k + \alpha r \bmod n$ which involves two secret values: the nonce and the private key. The part we will focus on is the random nonce $k$ : it must be random and chosen uniformly in the range $[1, n – 1]$ .

For information, the signature verification is as follows:

Verify that $r\in[1, 2^t - 1]$ and $s\in [1, n - 1]$ ( $t$ is the bit length of output of the hash function);

Compute $Q = [s]G - [r]P$ where $P$ is the public key of the signer;

Compute $v = H(Q_x, Q_y, M)$ ;

The signature is validated if $v = r$ .

Nonce generation

The analysis of the source code reveals that a Linear Congruential Generator (LCG) is used to generate the nonce in the sample_nounce() function that fills the buffer with 4 chunks of 64 bits each:

				
					/**
 * @brief Sample a 256-bit nounce using a LCG
 * 
 * @param nounce the output 256-bit nounce
 * @param lcg the LCG structure
 */
void sample_nounce(uint8_t nounce[32], lcg_t* lcg) {
    // Fill the four 64-bit chunks of pseudo-randomness
    uint64_t chunks[4];
    chunks[0] = next_64bits(lcg);
    chunks[1] = next_64bits(lcg);
    chunks[2] = next_64bits(lcg);
    chunks[3] = next_64bits(lcg);

    // Concatenate the chunks to get the nounce
    uint64_t* nounce64 = (uint64_t*) nounce;
    nounce64[0] = chunks[3];
    nounce64[1] = chunks[2];
    nounce64[2] = chunks[2];
    nounce64[3] = chunks[0];
}

Such a random generator is not suitable for cryptography: given an output of a LCG, it is possible to predict the next and previous ones.

The two parameters used for this LCG are: $\left\{\begin{aligned} a & = 6\,364\,136\,223\,846\,793\,005, \\ c & = 1\,442\,695\,040\,888\,963\,407. \end{aligned}\right.$

If $X_i$ is an output of the LCG, then the next one is (computed in the function next_64bits()): $X_{i+1} = a (a X_i + c) + c \bmod 2^{64}$

So, given an output $X_0$ , we can describe every following outputs as: $\left\{\begin{aligned} X_1 & = a_1 X_0 + a_0 \bmod 2^{64} \\ X_2 & = b_1 X_0 + b_0 \bmod 2^{64} \\ X_3 & = c_1 X_0 + c_0 \bmod 2^{64} \end{aligned}\right.$ The constants $a_0$ , $a_1$ , and so on are completely determined by the parameters $a$ and $c$ (example: $a_1 = a^2$ and $a_0 = ac + c$ ).

In the case of CRY-ME, four chunks are needed, and those are copied into a buffer nounce of 32 bytes. Though, a careful look at the code shows that one chunk is used twice so one is not used.

While it does not have an impact in the attack that is presented in this article, it would be bad in practice to have part of the nonce duplicated, and could lead to an attack.

So the nonce is constructed from three outputs $X_0$ , $X_2$ and $X_3$ , and those are concatenated into the buffer nounce in the order $X_3$ , $X_2$ (twice), and $X_0$ , where each chunk is in little-endian.

To have a visual representation, we note $X_i = x_{i,0} + x_{i,1}2^8 + \cdots + x_{i,7}2^{56}$ where the $x_{i,j}$ for $0 \leq j \leq 7$ correspond to the eight bytes of the chunk. Then, the buffer nounce indexed from $0$ to $31$ is given in the figure below:

Now, we need to understand how this buffer is interpreted as an integer in the scalar multiplication during the signature generation.

				
					// Extract of file `ecc_signature.c` lines 108-109:
    // Performs "Q = [k] G" where G is a curve generator
    wei25519_scalarmult_base(&point, k, SCALAR_BYTESIZE);

// Extract of file `wei25519.h` line 128:
    #define wei25519_scalarmult_base(out, sc, sc_bytelen) wei25519_scalarmult(out, &WEI25519_BASEPOINT, sc, sc_bytelen)

// Extract of the function `wei25519_scalarmult` in file `wei25519.c` lines 290-293
    // Montegomery Ladder
    for(int i=0; i<scalar_bytelen; i++) { // For each bit
        for(int j=0; j<8; j++) {
            char b = (scalar[i] >> (7-j)) & 1;

The constant SCALAR_BYTESIZE is 32 and corresponds to the size of the buffer containing the nonce, and corresponds to the scalar_bytelen in the for loop. We see that it starts from the first byte of the buffer (indexed from 0), and starts with the most significant bits of each byte.

The algorithm works by taking the bits of the integer from its most significant bits to the least significant bits. Thus, $x_{3,0}$ is the top byte of the nonce, followed by $x_{3,1}$ , etc. It means that the byte of each chunks are read in big-endian order.

Let $X'_i = x_{i,7} + x_{i,6}2^8 + \cdots + x_{i,0}2^{56}$ for $0\leq j \leq 7$ (all bytes in reversed order compared to the original $X_i$ ). Then, the nonce $k$ is the following integer: $k = X'_0 + X'_2(2^{64} + 2^{128}) + X'_3 2^{192}.$

It would have been simpler if the integer $X_0$ , $X_2$ and $X_3$ were used directly in the expression of the nonce $k$ . Anyway, what follows proves that it is still possible to exploit.

Now that we know what the nonce looks like, what do we do since we know it is completely determined by only 64 bits?

How many signatures do we need?

If we have the public key, then we run through all $2^{64}$ possible values for the nonce, and solve for the private key using the signature equation: it the public key matches, we have won.

Let’s start a thought experiment and suppose that we do not have the public key: how many signatures would we need to find the private key?

With one signature, running through all possible values for the nonce then we would end up with billions of billions of potential private keys. Without the public key, we could not know which one is correct. We could apply the same method for a second signature that would give us a second set of billions of billions of potentiel private keys, and the correct one should be at the intersection of both sets.

The probability that a value belongs to both sets is very low (except for the private key by construction). So two signatures should be enough.

Indeed, given a first set of $2^{64}$ potential private keys from the first signature, then each potential private key from the second signature has a probability around $p = 2^{64}/2^{255}$ to be in the first set. This situation can be assimilated to a binomial distribution of parameters $N = 2^{64}$ (number of draws using the second signature) and probabability $p$ , and its expected value is $Np = 1/2^{127}$ . (Of course, this is a bit of simplification, but it gives an idea of the order of magnitude.)

However, the analysis of the source code shows another interesting thing:

				
					// Extract of file `ecc_keygen.c` lines 30-34:
int wei25519_keypair(unsigned char* pk, unsigned char* sk, rnd_engine_t* rnd_engine) {
    wei25519e3_t point;

    // sample a random sk
    int res = wei25519_random_scalar(sk, WEI25519_SECURITYLEVEL_IN_BYTES, rnd_engine);

The number of bytes of the private key is controlled by WEI25519_SECURITYLEVEL_IN_BYTES which is 16 according to the following code:

				
					// Extract of file `ecc_h` lines 29-32:

// The security level (in bits) of the implemented primitives
#define WEI25519_SECURITYLEVEL 128
// The security level (in bytes) of the implemented primitives
#define WEI25519_SECURITYLEVEL_IN_BYTES (WEI25519_SECURITYLEVEL>>3)

The assertion is wrong: the security in bytes does not correspond to the key length for elliptic curves. The correct key size for 128 bits of security is 32 bytes, so the private key is half what it should be. Our previous reasoning can be applied again. Each potential private key from a single signature has a probability around

2^{128}/2^{255}

to be at most 128 bits. Out of the

2^{64}

potential private keys, we expect that no other value than the correct one should satisfy this condition: a single signature should be enough.

What remains to do is to find efficiently this private key from one signature.

Lattice attack

Lattices are great tools in cryptography: they are the basis of new cryptographic algorithms for post-quantum cryptography (CRYSTALS-Kyber, Falcon to name a few), and also good for cryptanalysis, in particular with partial key exposure (see Coppersmith’s method).

A lattice is a set of points where each point can be written as a vector containing its coordinates. They can be added or subtracted (coordinate by coordinate), or multiplied by an integer. A lattice can be represented by a matrix, where each vector is a combination of the rows of this matrix, using the rules given above. One difficult problem is to find short vectors of lattices (vectors with small coordinates).

The idea of lattice attacks in cryptography is to construct a lattice where a short vector contains the secret key or, at least, part of the secret key that is unknown, then use an algorithm such as LLL that finds a reduced basis with shorter vectors. If it is done right, one of these short vectors is the one we are looking for, containing the secret value.

Let summarize the situation:

The nonce $k$ is composed of 24 bytes: $x_{0,0}$ , $\ldots$ , $x_{0,7}$ , $x_{2,0}$ , $\ldots$ , $x_{2,7}$ , $x_{3,0}$ , $\ldots$ , $x_{3,7}$ ;
The private key $\alpha$ is less than $2^{128}$ .

This set of variables satisfies the following equations:

$s = k + \alpha r \bmod n$ , so there exists an integer $\lambda_1$ such that $s = k + \alpha r + \lambda_1 n$ ;
$X_2 = b_1 X_0 + b_0 \bmod 2^{64}$ , so there exists an integer $\lambda_2$ such that $X_2 = b_1 X_0 + b_0 + \lambda_2 2^{64}$ ;
$X_3 = c_1 X_0 + c_0 \bmod 2^{64}$ , so there exists an integer $\lambda_3$ such that $X_3 = c_1 X_0 + c_0 + \lambda_3 2^{64}$ .

We get the following system of linear equations: $\left\{\begin{aligned} k + \alpha r + \lambda_1 n – s & = 0 \\ b_1 X_0 + b_0 – X_2 + \lambda_2 2^{64} & = 0 \\ c_1 X_0 + c_0 – X_3 + \lambda_3 2^{64} & = 0 \end{aligned}\right.$

There are too many unknown variables in this system to solve it, but the three zeros on the right could be coordinates of a short vector of a lattice!

We can translate this system in a first matrix:

Multiplication on the left by the right vector gives the null vector. Next step is to add columns to put weights on the unknown variables:

$1/2^8$ for the values $x_{i,j}$ since they are bytes;
$1/2^{128}$ for the private key;
$1$ for the constant $1$ .

When multiplied by their weight, we get a number between 0 and 1 (very small, see the vector on the right).

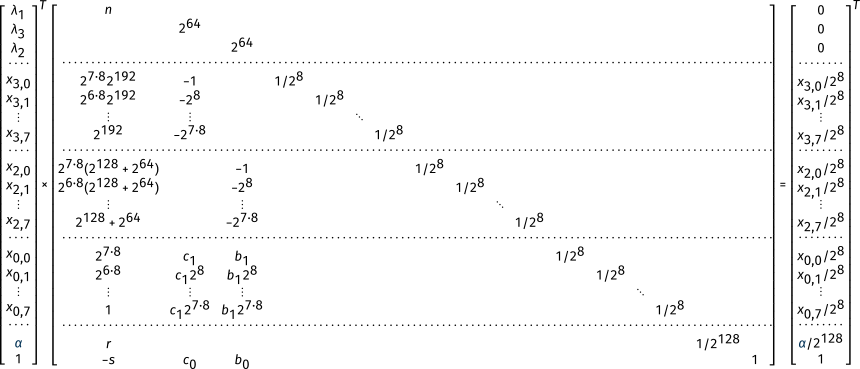
Notice that $\lambda_1$ , $\lambda_2$ and $\lambda_3$ do not have weights (we don’t care about those).

By construction, the vector on the right is short and contains the private key. Now we apply LLL on the matrix and this vector should appears as one of the rows of the resulting matrix. We look in the penultimate column to find the private key.

Example

To illustrate this attack, a simple program was written to sign one message with a private key. The public key and signature are given below encoded in base 64:

				
					Public key: IzGmYC1fTu3AEtHWR2oQMP0YiXIUYl1AWBXZ/6eSFYZCdWtgP7CUYuGVnOLPDOFT6uEb8vE5eXxYrc1RVgZEOg==
Signature: r5ysPYgq//ztVNhMsiXoG3L6gDVwm0eGYvhIB8u8N4wGHP4firfbbMGJM7bxtQ4s94HqlCkcMIsXf8i91sGRnw==

The lattice attack has been written in Python with fpylll and can be found in the Amossys Github repository.

The script break_schnorr.py takes the public key and signature as input and gives instantly the private key:

				
					python3 break_schnorr.py IzGmYC1fTu3AEtHWR2oQMP0YiXIUYl1AWBXZ/6eSFYZCdWtgP7CUYuGVnOLPDOFT6uEb8vE5eXxYrc1RVgZEOg== r5ysPYgq//ztVNhMsiXoG3L6gDVwm0eGYvhIB8u8N4wGHP4firfbbMGJM7bxtQ4s94HqlCkcMIsXf8i91sGRnw==
Public key: (0x2331a6602d5f4eedc012d1d6476a1030fd18897214625d405815d9ffa7921586, 0x42756b603fb09462e1959ce2cf0ce153eae11bf2f139797c58adcd515606443a)
Private key: 0xdfd421d217a6fd0db1629b9e1adade3

The 128-bit private key is recovered from a single signature!

Links

https://github.com/anssi-fr/cry-me

https://github.com/AMOSSYS/challenges/tree/main/CRY-ME/.

Voir les derniers articles de notre Blog technique

11 avril 2024

M&NTIS Platform est une solution SaaS destinée au test d'efficacité de produits de défense (AV, EDR, sondes réseau/NDR, SIEM, XDR, ...) et d'architectures de supervision. Une nouvelle version majeure de la plateforme vient de sortir.

25 mars 2024

Through this article, we propose a way to find LPE in Windows applications, by using SysInternals tools. What and how to look at? How to exploit in an easy and quick way?

4 décembre 2023

Find here the crypto and reverse challenges that our teams created for the European Cyber Week pre-qualification and qualification tests of CTF, a recognized cybersecurity event that took place in Rennes from November 21 to 23, 2023.

29 mars 2023

On the 24th of January, AMOSSYS and Malizen put together a Blue Team CTF, for the SupSec seminar organized by Inria. In this blog post, we explain how we, at AMOSSYS, generated the dataset used in this challenge.

20 décembre 2022

Find here the crypto and web challenges that our teams created for the European Cyber Week pre-qualification tests of CTF, a recognized cybersecurity event that took place in Rennes from November 15 to 17, 2022.

22 novembre 2022

Find here the write-ups of the crypto and web challenges that our teams created for the European Cyber Week pre-qualification tests of CTF

14 septembre 2022

This article starts with a quick overview on NIDS (Network Intrusion Detection System) evasions to remind what it is and why it could happen.

31 mars 2021

Essor du numérique, diversification des surfaces d’exposition, multiplication des cyberattaques… Depuis plusieurs années, la sécurité informatique est devenue une composante essentielle de l'administration d'un Système d'Information (SI).

18 septembre 2020

Depuis plusieurs années, l'écosystème informatique a dû faire face à une recrudescence de compromissions de systèmes d'informations par des rançongiciels, ou cryptolockers, qui s'introduisent principalement par des méthodes automatiques (_spear phishing_, etc.).

12 août 2020

We will discuss the feasibility in real world of the Spectre V1 flaw from a cross-process, userland perspective.

Vous souhaitez :

Toutes nos prestations

Tous nos produits

Qui sommes-nous ?

Nos marchés

Vous êtes victime d’un incident de sécurité ? Contactez notre CERT

Blog technique