04/06/2024
Blog technique
Why you should not put all your eggs in the same basket | Part 3
Lucile Razé & Gabriel Departout
Why you should not put all your eggs in the same basket.
A series about post-quantum cryptography
Part III: Hybridization’s DIY Tutorial
Welcome to the last part of this blog series about hybridization. In the first part here, we introduced why using quantum computer can threaten classical cryptography. In the second blog post, we presented a practical solution to the quantum threat, namely hybridization. This blog post will be more technical than the previous ones, we recommend you to read them before get into this one. The goal here is to give you the main methods to build hybrid KEM, PKE and digital signatures properly. These combiners come from the scientific literature, so they have been peer reviewed. For each primitive, we are going to give its target security and two viable combiners.
Key encapsulation mechanism combiners
Security
As depicted in the previous blog post, a KEM is an asymmetric cryptographic primitive used to exchange a secret key between two parties. Let’s consider K = ( KeyGen , Encaps , Decaps ) a KEM as defined in the second blog post, how can we be sure that K is secure? And what does it mean to be secure for a KEM?
A KEM is said to be secure if an attacker A cannot distinguish the real secret key shared using K from a random one in a reasonable time (less than 2256 classical elementary operations and less than 2128 quantum elementary operations). To do so, the imaginary attacker A can do queries to a decapsulation oracle: a black box that returns the key corresponding to the input ciphertext. If A does not succeed, the KEM achieve Key Indistinguishability under Chosen Ciphertext Attack (IND-CCA) security.
One can define a weaker variant of this security where the attacker does not have access to a decapsulation oracle (but he can still use Encaps because the only material needed is the public key, which is public): this is the IND-CPA security (Chosen Plaintext Attack). Notice that if the KEM is IND-CCA secure then it is also IND-CPA secure.
XOR combiner for KEM
After having generated a key pair with KeyGen and establish a shared secret k, it seems logical to throw away the key pair generated, we call them ephemeral keys. When using ephemeral keys, IND-CPA security is enough for your KEM (NIST, 2016). Here we are going to present a KEM combiner that preserves IND-CPA security. But first, let’s define a hybrid KEM.
Let K1 and K2 be two KEM and their associated functions KeyGeni, Encapsi and Decapsi. We define the hybrid KEM K and its associated functions as follow:
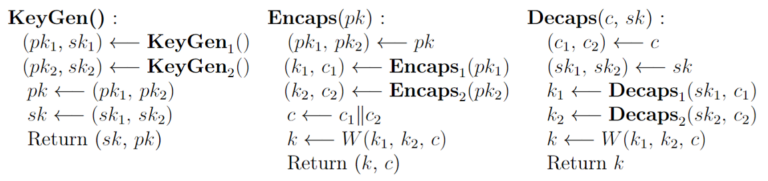
Where combined pki and ski are resp. the public and the private keys of the scheme Ki , W is a combiner who takes as input the two secret keys k1 and k2 established with each KEM and the combined ciphertext c = c1 || c2 and output the combined shared secret k. Now we can define our first combiner. We can define the hybrid KEM XOR ( K1 , K2 ) and its combiner by
W ( k1 , k2 , c ) = k1 ⊕ k2
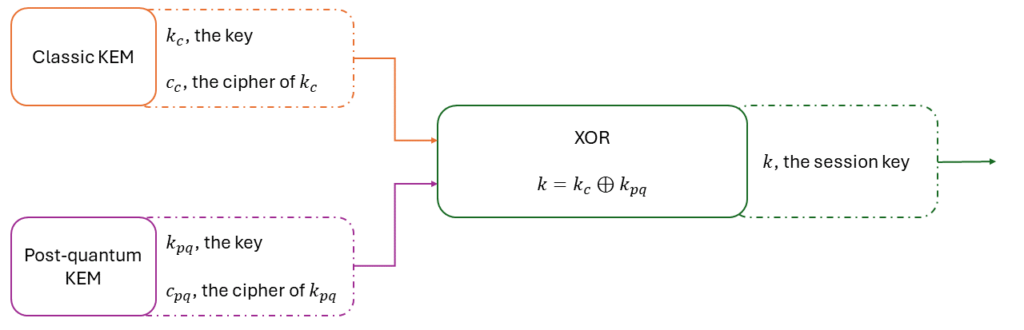
If K1 or K2 is IND-CPA secure, then XOR ( K1 , K2 ) is IND-CPA secure. The XOR combiner is a very simple and robust way to hybrid KEM when using an ephemeral key pair. You can for instance combine KYBER-1024 with DH-KEM (the KEM version of the Diffie-Hellman protocol) using the combiner to get an IND-CPA hybrid KEM (because both underlying KEM are IND-CPA).
CatKDF combiner
Now a combiner for the IND-CCA security. We define the hybrid KEM CatKDF ( K1 , K2 ) and its combiner by:
W ( k1 , k2 , c ) = KDF ( k1 || k2 )
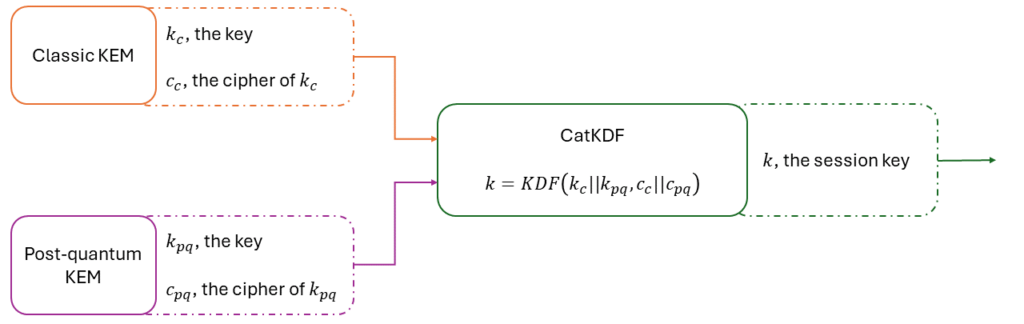
where KDF is a secure key derivation function (like HKDF for instance). If K1 or K2 is IND-CCA secure, then CatKDF ( K1 , K2 ) is IND-CCA secure. Note that the parameters of the KDF function must take into account the combined ciphertext in its process. For instance, in HMAC-based KDF function (IETF, 2010), one need a salt to derive the secret, this salt could use the ciphertext as the random seed. Otherwise, one can attack the IND-CCA security of the hybrid KEM under certain assumptions about the malleability of K1 or K2 (assumptions that El-Gamal satisfies). The CatKDF combiner has been selected for the hybrid key exchange in TLS 1.3 (Gueron, 2024).
Public key encryption combiner
OW-CPA security
As depicted in the first blog post, a PKE is an asymmetric cryptographic primitive E = ( KeyGen , Encrypt , Decrypt ). We will see later how one can build a secure KEM based on a PKE. But first we need to introduce the security notion of One-Wayness under Chosen Plaintext Attack (OW-CPA). The idea is simple: can an attacker recover the plaintext from the ciphertext in a reasonable time? If not, the PKE is said OW-CPA secure. Every PKE must be at least OW-CPA secure (otherwise we strongly advise you not to use it).
XOR combiner for PKE
Let E1 and E2 be two PKE and their associated functions KeyGeni , Encrypti , and Decrypti .We define the hybrid PKE XOR ( E1 , E2 ) as follow:

Where m1 is a random message picked from the messages space M.
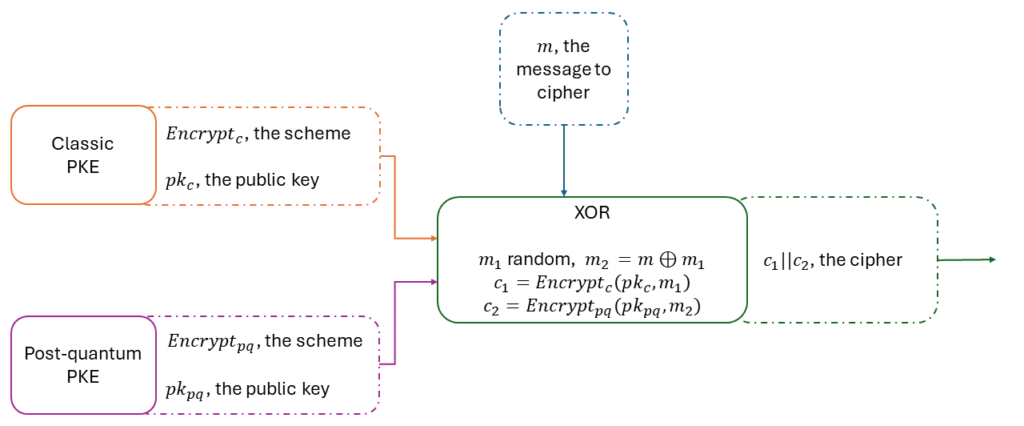
If E1 or E2 is OW-CPA secure, then the PKE XOR ( E1 , E2 ) is OW-CPA secure.
FO transforms
This is quite nice already but remember: KEM is the new trend. Here is the plan, from our two PKE E1 and E2 OW-CPA secure, we managed to get a hybrid PKE E OW-CPA secure thanks to the XOR combiner for PKE described previously. Now we want an IND-CCA KEM. In (Kiltz, 2017), one can find what we call the Fujisaka-Okamoto transforms. These transformations, when combined properly, allow you to build an IND-CCA KEM from an OW-CPA PKE. This is exactly what we need. Here we present you the final construction which is a KEM K ( E1 , E2 ) .

Where H is a secure hash function (it has the role of a pseudo-random function. In the end, K ( E1 , E2 ) is IND-CCA secure if E1 or E2 is OW-CPA secure. This method is less documented in the literature, one can get more information here (Kiltz, 2017). Indeed, all the implementations proposed for the post-quantum schemes of the NIST competition are for the KEM and not for the underlying PKE. That may be the reason the first method is preferred.
Signatures combiners
EUF-CMA security
Last but not least, we have digital signatures. As a reminder, a signature is an asymmetric primitive S = ( KeyGen , Sign , Verif ) used to authenticate the party associated to a key pair. A signature scheme is secure if it’s impossible for an attacker A to forge a valid signature σ for a message m chosen by A in a reasonable time, even if A can query a signing oracle (a blackbox that signs an input message, but not m, it would be too easy). This is called the Existential Unforgeability under Chosen Message Attack (EUF-CMA) security.
CAT combiner for signatures
Let S1 and S2 be two signature schemes and their associated functions KeyGeni , Signi and Verifi , as defined in the second blog post. We define the hybrid signature CAT ( S1 , S2 ) as follow:

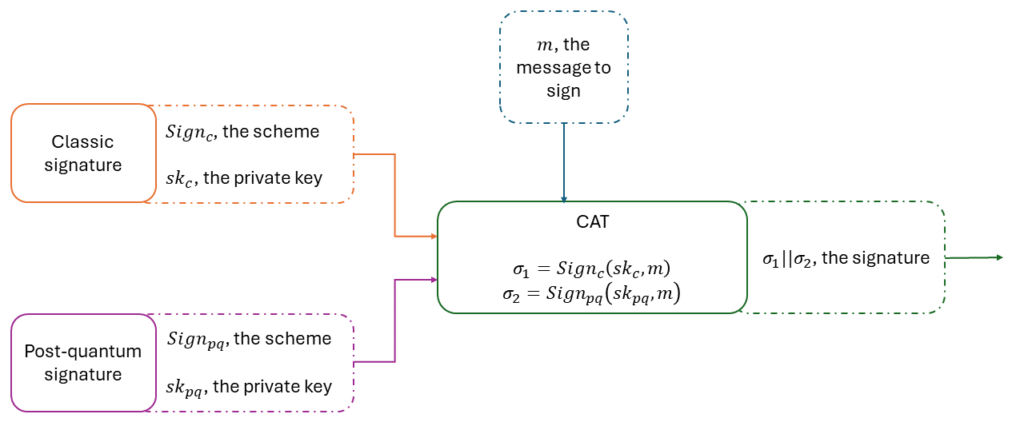
If S1 or S2 is EUF-CMA secure, then the hybrid signature CAT ( S1 , S2 ) is EUF-CMA secure. You can for instance combine FALCON-1024 and ECDSA using the CAT combiner to get a EUF-CMA hybrid signature, because both underlying schemes are EUF-CMA.
The CAT combiner is simple, maybe too simple. Let’s imagine the following scenario: Alice wants to sign a document m for Bob. Bob accepts hybrid signatures combining ECDSA and Dilithium, but in a transition context he may also accept only ECDSA signatures. Let σ be the hybrid signature σDSA || σDltm of m sent to Bob. Consider Eve, who spies on the channel between Alice and Bob and can modify the content of packets before retransmitting them. When Eve sees σ passing by, she can extract σDSA , which is a valid signature for m , and only retransmits it to Bob. This means that the signature Bob receives is not post-quantum, which was not Alice’s original intention. Indeed, using a quantum computer, Eve could alter m while keeping σDSA valid. The next combiner we propose counter this downgrading attack.
Strong Nesting combiner
Let S1 and S2 be two signature schemes and their associated functions KeyGeni , Signi and Verifi . We define the hybrid signature StrNest ( S1 , S2 ) as follow:

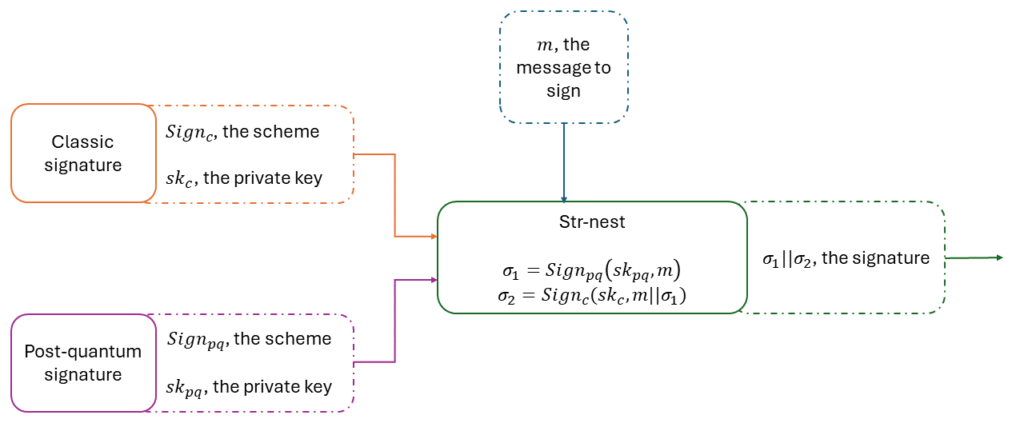
If S1 or S2 is EUF-CMA secure, then the hybrid signature StrNest ( S1 , S2 ) is EUF-CMA secure. One can notice that you can still extract the valid signature S1 from the combined signature σ . That’s why we recommend S1 to be the post-quantum scheme, to assure at least the post-quantum security in the case of a downgrading attack.
What you should remember
In this blog series, we first depicted the consequences of the upcoming of the quantum computers for cryptography.
Hybridization seems to be the perfect solution to the tricky choice between choosing a post-quantum scheme that we cannot trust yet, or choosing a classic scheme we know well but that will probably be broken in one or two decades.
Just do not rush into standalone post-quantum protection for the moment, think hybridization. The ITSEF of AMOSSYS will be ready to advise you and assess products that use post-quantum cryptography by 2025. You can always come to say hello.
References
Gueron, D. S. (2024). Hybrid key exchange in TLS 1.3. IETF. https://www.ietf.org/archive/id/draft-ietf-tls-hybrid-design-09.html
IETF. (2010). HMAC-based Extract-and-Expand Key Derivation Function (HKDF). https://datatracker.ietf.org/doc/html/rfc5869
Kiltz, D. H. (2017). A Modular Analysis of the Fujisaki-Okamoto Transformation. https://eprint.iacr.org/2017/604
NIST. (2016). Call For Proposal. https://csrc.nist.gov/CSRC/media/Projects/Post-Quantum-Cryptography/documents/call-for-proposals-final-dec-2016.pdf









