04/06/2024
Blog technique
Why you should not put all your eggs in the same basket | Part 1
Lucile Razé & Gabriel Departout
Why you should not put all your eggs in the same basket.
A series about post-quantum cryptography
Part I: A Post-Quantum World
In the world of cybersecurity, “post-quantum cryptography” start to be on everyone’s lips, and it’s not about to slow down. Indeed, according to the BSI’s report (BSI, 2021), quantum computers that pose a real threat to today’s cryptography are expected to be here in the early 2030s. Of course, it’s unlikely that we’ll all have quantum computer one day. At first it will be nation states or multinational companies that will have access to this technology. The rest of us will keep on using “classic computers”. This the post-quantum model; classic computers must protect themselves from a few quantum computers. But what do we mean when we talk about the post-quantum cryptography? What is exactly at stake? In this first blog post, we will try to answer these questions and see that post-quantum cryptography is not a swear word.
Quantum computers
Unfortunately, we will not explain how a quantum computer does work today. Nor tomorrow. To sum up, just remember that a quantum computer uses qubits instead of classical bits. A qubit is the smallest unit of quantum information storage. Unlike a bit, which is always in a definite state of either 0 or 1, a qubit can exist in superposition, meaning it can be in a combination of both states simultaneously (CEA, 2018). A qubit can be encoded by the polarization of a photon or the spin of an electron for instance. Just like with bits, qubits can be manipulated using logic gates to modify the information they contain. With a significant number of qubits, this gives you a new world of possibilities to handle information in the execution of an algorithm. It looks like magic, but there are some technical issues of course (what did you expect). That’s why there are billions of dollars invested every year in this field of research.
So, ideal quantum computers are powerful, they can do some things a classical computer can do, but much faster. Let’s take the simple case of an algorithm that must find and return a specific element in an unstructured list. For a classical computer, if the size of the list is n, you’ll need about n elementary operations to find the element (or not), because you’ll have to check each element individually. For a quantum computer, you’ll need only √n elementary operations to find the element you’re looking for with high probability. That’s quite an optimization, especially if you want to find a secret key in a very large set of possible keys (we will come to that later). For the record, this first algorithm is called Grover’s algorithm (Grover, 1996).
Symmetric cryptography
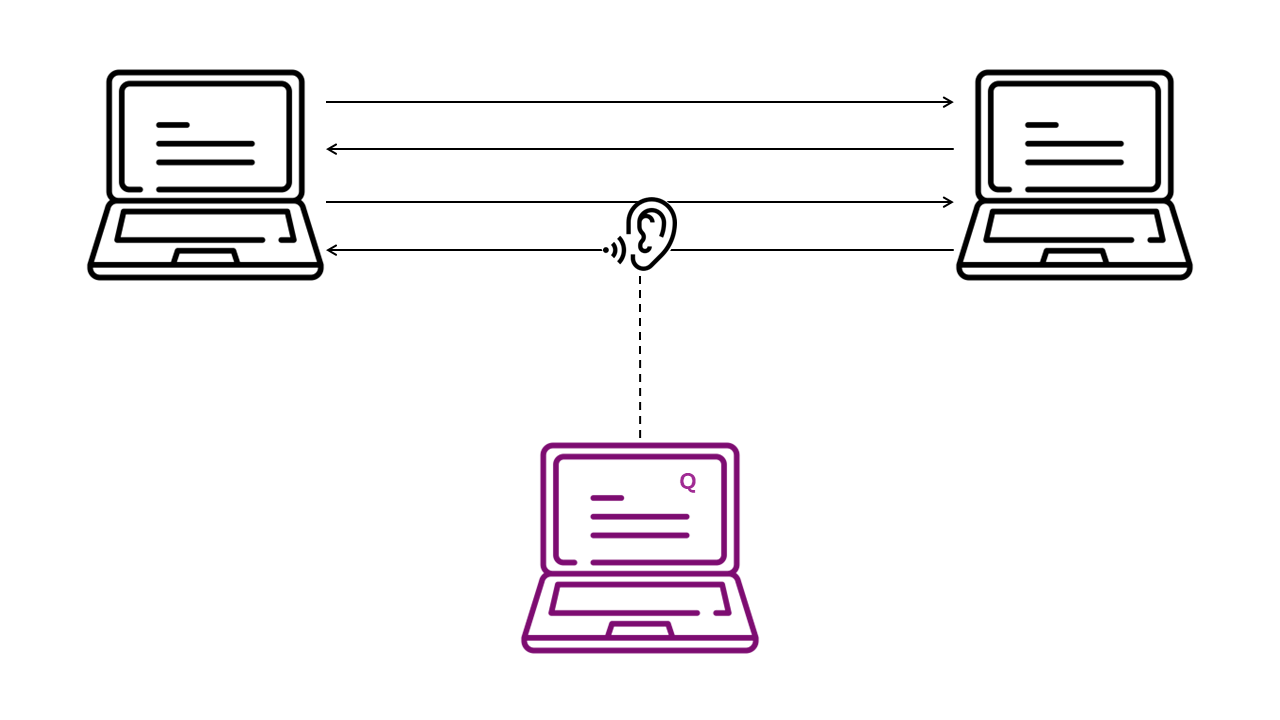
To understand why quantum computers are a threat for cryptography used every day, we need to return to the basis, namely the difference between symmetric and asymmetric cryptography. We talk about symmetric cryptography when the same key is used to encrypt and decrypt data. Let’s take the case where Alice and Bob have previously shared a secret key in a trusted way, for example in person. They can now use this same key for both ciphering and deciphering messages using a suitable algorithm.
Asymmetric cryptography
Now for the asymmetric part. In the previous example, you may wonder how did Alice and Bob share this secret key. It’s hard to meet everyone in person. This is where asymmetric cryptography comes into play.
Public Key Encryption (PKE) works as following. Imagine Alice wants to send Bob a message, but they do not have any shared secret. Bob generates two keys: a public one pk and a private one sk. To send Bob a message m, Alice only needs Bob’s public key pk and an encryption function to encrypt the message.
Encrypt ( m , pk ) = c
Now Bob receives the ciphertext c and wants to recover m. To do so he only needs his secret key sk and a decryption function.
Decrypt ( c , sk ) = m or Error
Attackers who want to decrypt c can simply not because they do not know sk.
As an example of PKE we’ll use the RSA algorithm. Let’s take p and q two prime numbers. We note n := p X q. If I give you p and q it’s easy for you to construct n, you just have to do a simple product. However, if I give you an extremely large n and ask you to recover p and q from it, you may have some difficulties given that even a computer struggle to solve this problem. You got the idea, it’s easy in one way, hard in the other unless you have a “trapdoor” to recover the information (in this case knowing p or q allows to recover the other). This is called a trapdoor one-way function. The problem described above is called the factorization problem. If one can solve the factorization problem in a reasonable time, one can break RSA cryptosystem. In RSA, the public key is pk := n and the secret key is sk := ( p , q ). But do not misunderstand, the functions Encrypt and Decrypt of RSA are not the factorization problem per se, they are just based on it.
In the above description, encrypting a message would be the easy part of our one-way function. Decrypting a message would be the hard part of our one-way function. Fortunately for Bob, he has a trapdoor to inverse the function; his secret key sk.
Nowadays, the size of n is about 10920 (a number with 920 decimal digits) and it takes around 2128 elementary operations to solve the factorization problem with the best generic attack: on a mainstream processor (1GHz), this would take about 1027 seconds or 33 trillion of years.
If you wonder how one can be sure that Bob’s public key is indeed Bob’s public key and not an impostor’s, there are solutions with additional structures like certificates and Public Key Infrastructure (PKI). But remember that you’ll have to trust a third-party at some point. Here is some reading about it (Wikipedia).
Shor's algorithms
We can mention another hard problem for classical computers, namely the discrete logarithm problem in elliptic curves. It’s more used than RSA, but harder to explain, so we won’t go into it, don’t worry. These two problems are the ones used everywhere today to build PKE and exchange secret keys. Unlike symmetric cryptography, asymmetric cryptography is more expensive (in terms of time of execution). Moreover, one-way functions rely on structured mathematical theories, and thus are more sensitive to attacks. That’s why we only use it to exchange secret keys to do symmetric cryptography. In 1994, Peter Shor published a paper (Shor, 1994) describing three quantum algorithms capable of solving the factorization and the discrete logarithm problems in a realistic time for a quantum computer. In the above example, it would take only 235 elementary operations (quantum gates) for a quantum computer to solve the factorization problem, which is much lower than 2128, the tolerated lower bound by the NIST and the ANSSI. You see the problem now. Imagine that Eve wants to spy messages between Alice and Bob who use RSA to communicate. Even if Eve does not have access to a quantum computer now, maybe she will in 20 years. If she stores all the encrypted communications of Alice and Bob, she will be able to break them in the future. That’s the mantra “Harvest Now, Decrypt Later”.
In the same way, Grover’s algorithm, mentioned earlier, can be used to guess symmetric keys faster. However, the countermeasure is easy in this case: doubling the size of symmetric keys. There’s no need to invent new mathematical problems.
New standards
In 2016, the US National Institute of Standards and Technology (NIST) launched an international competition in order to find replacements for RSA and elliptic curves-based algorithms. We have some promising candidates such as Kyber and BIKE for Key Encapsulation Mechanism (KEM) and Falcon and SPHINCS+ for digital signatures. These algorithms rely on supposed hard problems (even for a quantum computer) of the lattice’s theory or correction codes theory (except for SPHINCS which is a Hash-Based Signature). But, there is a but. An important ingredient in the security of a mechanism is the test of time. We don’t have enough hindsight on these algorithms to rely only and completely on them, as demonstrated by the case of SIKE, a promising algorithm of the NIST’s competition eliminated in 2022 following the publication of a key-recovery attack (Decru, 2022).
To conclude, on the one hand we have the cryptography currently used that will be soon obsolete because of quantum power. On the other hand, we have post-quantum algorithms too young to be fully trusted. Seems to be a dead end…
References
BSI. (2021). Quantum-Safe Cryptography. https://www.bsi.bund.de/SharedDocs/Downloads/EN/BSI/Publications/Brochure/quantum-safe-cryptography.html
CEA. (2018). Le calcul et l’ordinateur quantiques. https://www.cea.fr/comprendre/Pages/nouvelles-technologies/essentiel-sur-ordinateur-quantique.aspx#:~:text=Le%20bit%20quantique%20ou%20qubit,0%3E%20et%20%7C1%3E.
Decru, W. C. (2022). An efficient key recovery attack on SIDH. https://eprint.iacr.org/2022/975.pdf
Grover, L. K. (1996). A fast quantum mechanical algorithm for database search. https://arxiv.org/pdf/quant-ph/9605043.pdf
Shor, P. (1994). Algorithms for Quantum Computation: Discrete Logarithms and Factoring. http://cc.ee.ntu.edu.tw/~rbwu/rapid_content/course/QC/Shor1994.pdf
Wikipedia. (s.d.). Public key infrastructure. https://en.wikipedia.org/wiki/Public_key_infrastructure









