14/01/2020
Blog technique
Linux RNG architecture
Guillaume Gauvrit
Focus on the architecture of the Linux random number generator, also known as `/dev/urandom`. How does it work? Is it secure? Shouldn’t I use `/dev/random`? All those questions and more are answered in this article.
Introduction
The Linux CSPRNG (cryptographically secure pseudo-random number generator) is one of the most used source of randomness. Its soundness is thus of critical importance for applications using cryptography, such as SSH, web servers or VPN servers. However, the CSPRNG’s official documentation might be a bit difficult to digest. This blog article documents its inner workings, focusing on the most important points, so that anyone can easily assess whether the generator meets their requirements and which of its interfaces should be used.
Overview
Because a picture is worth a thousand words, the following figure presents the architecture of the Linux CSPRNG. On top are the randomness (or noise) sources. The squared blocks represent memory structures holding the randomness data. Under Shannon’s information theory, they are named random variables, whose random information content is measured in entropy bits. At the bottom, the four userland interfaces that can be used to access the CSPRNG output are represented in rounded blocks.
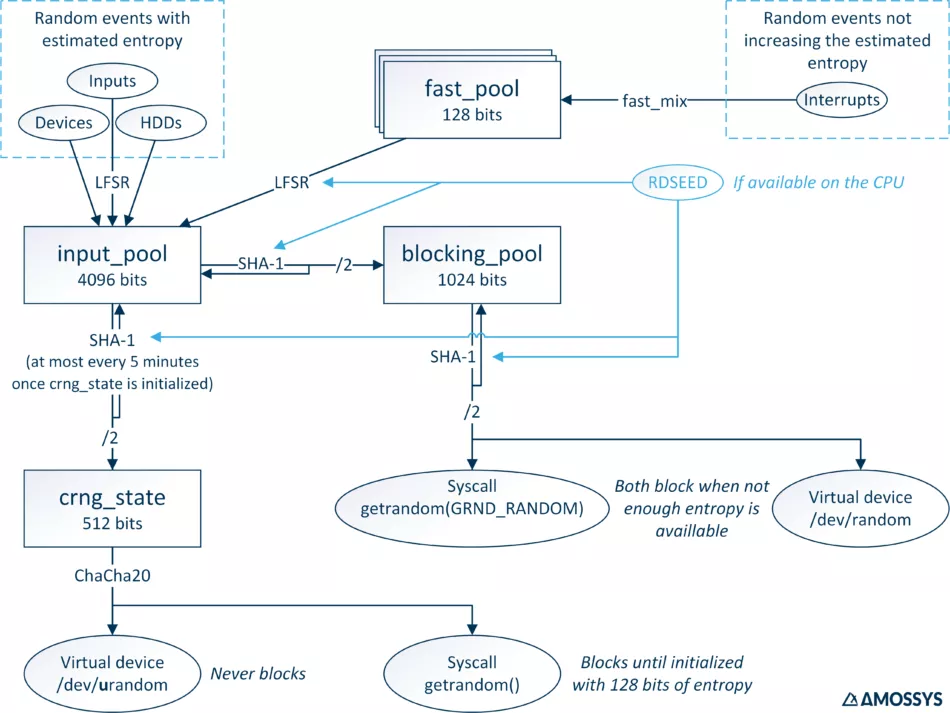
Figure 1: Linux CSPRNG architecture overview
The architecture presented here is accurate for the Linux kernels from version 4.18 to at least version 5.4 (the kernel’s version at the time of writing). The CSPRNG’s source code [1] is regularly updated. In particular, in version 4.8, its architecture has been reworked by replacing the output of /dev/urandom with data coming from a stream cipher instead of directly from a randomness pool. In order to understand the precise workings of the generator in a specific kernel version, nothing beats reading directly the source code. That’s why the names of the main functions and structures are given in this article. However, hopefully this article will make it easier to understand the source code.
Aggregation of random data into pools
The random data collected by the operating system (such as the access time to the HDD, some network data, the mouse’s movement or the key strokes) is used as an entropy source (see Section Entropy Sources). This data is aggregated in a pool of 4096 bits, named input_pool. This aggregation process uses a fast algorithm because the quality of the generated data is not ensured by this step. Furthermore, this process should not noticeably slow down the system. This mixing algorithm is a LFSR (linear-feedback shift register), implemented in the function _mix_pool_bytes(). The aggregation is a little more complex for random data extracted from interrupts. Because they are very frequent and only a few bits can be extracted in that manner, an even faster algorithm, a kind of checksum, is used to store entropy in small intermediary pools named fast_pool (one per CPU core), in the function fast_mix(). When enough data has been collected, those pools’ contents are mixed in the input_pool, without increasing its estimated entropy (contrary to the other sources), unless the CPU provides the RDSEED instruction. In this case, the output of RDSEED is also mixed in the input_pool and its estimated entropy is increased by 1 bit. The amount of entropy included in the inputs is estimated in a conservative fashion (it is very underestimated [2][3]). This measurement is added to the pool’s entropy, limited by its size. This estimation is reduced by the number of bits read (extracted) from it. No data in input_pool can be accessed by the user. Its data can only be automatically extracted to be mixed into two other pools, blocking_pool and crng_state.
A second pool is the blocking_pool. It shares the same structure as the input_pool, only with a reduced size of 1024 bits. When reading from this pool, it transfers as much entropy as needed from the input_pool, using the extraction algorithm described in the next section. Every byte read in this way is mixed, one by one, into the blocking_pool until as many bytes as needed are mixed (no more, no less). The measurement of entropy of the input_pool is reduced from the number of read bytes and the one of the blocking_pool is increased equally. Then the data is extracted from the blocking_pool using the same extraction algorithm and its entropy measurement is decreased of the amount extracted. This extracted data can be read by the user either by reading the special device file /dev/random or by calling the syscall getrandom() with the flag GRND_RANDOM. By default, reading from the blocking_pool is prevented until enough entropy is gathered in its inner state; using the flag GRND_NONBLOCK returns an error instead of blocking. The minimum amount of entropy to store in this pool can be changed by writing into the special file /proc/sys/kernel/randomread_wakeup_threshold.
A third entropy buffer is the inner state of the CSPRNG, crng_state, of 512 bits. No entropy measurement of its inner state is performed. Its initialization is done by extracting data from the input_pool, again following the extraction algorithm described in the next section. For efficiency’s sake, once this generator is initialized, the extraction of data from the input_pool is performed at most every 5 minutes (when no data is needed, none is extracted). Reading data from the crng_state is done using a stream cipher, Chacha20, which is faster than using a hashing function as it is done in the entropy extraction algorithm. Reading the output of the cipher can be done either by reading the special device file /dev/urandom (notice the « u », meaning « unblocking ») or by calling the syscall getrandom() without flags. Reading from this /dev/urandom is never blocking, whatever the intrinsic entropy of the crng_state. However, calling getrandom() is blocking until the crng_state is initialized by extracting 128 bits from the input_pool (by the function crng_reseed()) or until it is initialized with 512 bits (by the function crng_fast_load()[4]) from interrupts or the CPU’s hardware generator (if available). There is no risk of « running out » of entropy using either /dev/urandom or getrandom(). The time delta of 5 minutes is short enough to reseed the state before the stream cipher repeats itself, even in worst case scenarios.
Entropy extraction algorithm
The entropy extraction from a pool is always done with the same algorithm, by the function extract_buf() (except from fast_pool which are more akin to local buffers used in a function). A SHA-1 hash of the pool’s data is computed, that is 160 bits, which are immediately mixed back into the pool to avoid backtracking attacks, using the algorithm described in the next section. Then, this hash is « folded » back on itself (XOR of the 80 MSB onto the 80 LSB) and only this half hash is outputted. When the CPU provides the instruction RDSEED, the initial state of the SHA-1 algorithm is initialized with it, thus mixing hardware-generated random data into the pool and the extracted data. The entropy extraction is thus done in blocks of at most 80 bits. Moreover, every extraction shuffles the inner state of the pool. Overall, this algorithm is rather slow because it uses SHA-1. The use of a cryptographic hash ensures a uniform distribution of the output (reading) indistinguishable from random data, which allows to use without risks a fast mixing function when inputting (writing) into the pool.
Pool mixing algorithms
Data inserted into pools is mixed one byte at a time using a LFSR by the function _mix_pool_bytes(). The LFSR is defined by two different polynomials depending on the pool:
- x128 + x104 + x76 + x51 +x25 + x + 1, for the
input_pool - x32 + x + x19 + x14 + x7 + x + 1, for the
blocking_pool
In particular, this algorithm is used when adding fresh data from events, but also when extracting data from a pool, to shuffle it to prevent backtracking attacks, as explained in the previous section.
Pools initialization
When the kernel boots, before receiving any event or being seeded with a previously saved state, the inner state of the input_pool and the blocking_pool is a random number generated at compile time by the GCC plugin « latent_entropy ». Then, the pools are initialized by the function rand_initialize(): first the input_pool and the blocking_pool, then the crng_state is initialized from the output of the input_pool. When the operating system is shut down, the inner state of the pools should be saved into /var/lib/random-seed (only readable by root), to be restored at the next reboot. This behavior is not enforced by the kernel and depends on the configuration of the Linux distribution.
The data used at boot time to initialize the input_pool and the blocking_pool is:
- The current time and date.
- If the CPU provides a hardware random number generator, then it is used to fill the pools.
- The UNIX name of the computer, including:
- the name of the OS (for example « Linux »),
- the domain name is possible,
- the release number,
- the version number,
- the architecture name.
This initialization does not increase the estimated entropy of the pools, which is still 0 at this step.
A study [3] by the BSI details how a Linux system boots, without limiting itself to the kernel. Quoting this study:
1. The system is powered on, and the kernel is loaded into memory and boots.
2.Either in the very late stages of the kernel boot or during the first steps of the initramfs user space boot operation, the first four fast_pools are injected into the ChaCha20 DRNG to bring it into an initially seeded state.
3. After ending the initramfs phase which mounted the root file system, the user space initialization starts. During the early phase of this initialization, the seed file is written into /dev/random.
4. SSH server daemon, web servers with TLS support, and the IKE daemon start. During their startup, the used cryptographic libraries seed their DRNG from /dev/urandom. Those daemons are accessible from remote entities and are intended to grant secure cryptographic operation. Note, those user space DRNGs either do not reseed automatically at all (like it is the case with OpenSSL's SSLeay DRNG) or only after a large reseed interval (in cases like SP800-90A DRBGs, or libgcrypt's CSPRNG). This means that by the time the daemons start and initialize their DRNG, sufficient entropy must be present in the Linux-RNG as these daemons must be considered to be cryptographically insecure otherwise.
5. Far later than the completion of the user space initialization, the input_pool is filled with 128 bits of entropy for the first time. To give readers an impression about the delay in a worst-case, the author installed a Fedora 25 system in a virtual machine with hardly any devices. Although the ChaCha20 DRNG initial seeding step was reached after about 0.9 to 1 seconds after boot, the fully seeded stage that marks the receipt of 128 bits of entropy in the input_pool was reached up to 90 seconds after boot. The boot process of user space with an SSH daemon was fully completed after 2.5 seconds.
Entropy Sources
The Linux kernel uses four sources of random data, to feed the input_pool:
The function add_device_randomness() adds entropy from data that likely differ between devices, such as MAC addresses and serial numbers. This function does not increase the estimated entropy in the pools. It is used to initialize the pools and is mostly useful for systems with few randomness sources available, such as embedded systems.
The function add_input_randomness() uses the timestamp (jiffies) and the “type” (an unsigned integer) of hardware events.
The function add_disk_randomness() uses the time to access the hard drives. SSD are not a good source of entropy because this time is relatively constant for them, because they don’t use moving parts and thus have no random seeking time that depends on the position of the plater. This function is disabled at compile time when the support for the block layer is disabled, typically in some embedded devices.
The function add_interrupt_randomness() saves data from interrupts (timestamp, memory address of the calling function, code and flags of the interrupts, totaling 128 bits) in a fast_pool of 128 bits (one per CPU core), by XORing the new data with the pool’s state. Then, this state is mixed with fast_mix(), which is faster than the LFSR used by the other pools. The content of this fast_pool is used once per second to add entropy to the input_pool. This function does not increase the entropy measurement, unless the CPU provides a hardware RNG. In this case, a long from this generator is mixed, but the entropy estimation is only increased by one bit.
The estimation of the amount of entropy in a timestamp is computed by taking the number of ticks (jiffies) between two events. The minimum value of the 3 last deltas is divided by two, then the number of bits needed to represent this number is measured (i.e. $log_2(n) + 1$ if $n > 0$). This value, which can be 0, is maxed by 11 and then added to the estimation of entropy of the input_pool.
A study2 by the BSI evaluates the quality of the entropy sources in a VM. No tested configuration was pathological: they all had at least one source of adequate quality. The estimation of the entropy amount remains valid. The only weak point is when cloning VMs: the initial state of the VM is then the same when they are just cloned and the output of /dev/urandom is no longer reliable. A solution is to use the function get_random() which blocks until the CRNG state has been refreshed with 128 new bits of entropy. The same issue appears when starting or cloning snapshots of running VMs, however in this case no solutions are provided to ensure that the pools are refreshed after restoring a snapshot.
Random data generation for the kernel
The kernel can use 3 other functions to generate random data:
get_random_bytes()generates any amount of data, using the same output as/dev/urandom, without blocking.get_random_u32()andget_random_u64()to generate 4 or 8 bytes. They replaceget_random_int()andget_random_long(). They also use the same output as/dev/urandom, without blocking and this time without backtracking protection. If the CPU provides the RDSEED instruction, it is used instead, without reading from any pool. Those functions are meant to be used when their output is not critical, meaning that it is never exposed to userland.
Quality and soundness of the Linux PRNG
To be cryptographically secure, the pseudo-random number generator must satisfy the following robustness properties [5]:
- Resilience: The output must be indistinguishable from random data to an observer without knowledge of the inner state of the PRNG, even if the attacker has complete control over the data used to refresh the RNG state. This implies that it must be computationally impossible to enumerate all the possible inner states of the generator. I.e., a compromise of the refresh data is not enough to predict future output.
- Forward secrecy (or backtracking resistance): An observer that learns the inner state of the PRNG must not be able to distinguish past output from random data. I.e., a compromise of the state is not enough to discover previous output.
- Backward secrecy (or self healing, or break-in recovery): An observer that learns the inner state must not be able to distinguish future output from random data, provided that the generator is refreshed with data of enough entropy. I.e., a compromise of the state is not enough to predict future output.
In the Linux PRNG, the resilience property is ensured with the extraction function, using the (folded) one-way function SHA-1, and assured a second time (only for the unlocking output) by the use of a stream cipher. The size of the pool ensures that the enumeration of all their possible states is computationally impossible, even for quantum computers (the pools’ sizes are greater than 256 bits). The forward secrecy property is ensured by the backtracking protection, done by mixing back the output of the (unfolded) one-way function SHA-1 into the pools on every data extracted from the pools. The backward secrecy property is ensured by constantly refreshing the state of the pools with new random data. The estimation of the entropy of this data is done conservatively (i.e. underestimated), even though one could argue [5] with the computation formulae and the usefulness of an entropy estimation. Since the state of crng_state is refreshed every 5 minutes, the self-healing or recovery time of the /dev/urandom output is 5 minutes.
Researchers discussed [5] the generation of pseudo-random data and the estimation of the entropy in the implementation of the Linux PRNG in versions prior to 4.8. Their conclusions have been taken into account in newer versions of the kernel: the output of /dev/urandom is taken from a stream-cipher whose state is refreshed every 5 minutes (as suggested [5]). They also state that any kind of entropy estimation is at best bogus and mostly unnecessary in practice. Should an estimation be made, it should be very conservative. This blog article author believes that the entropy estimation performed (often estimating to 0 additional bit) is conservative enough.
Another article [6], in which the version implemented in kernel 3.7.8 was studied, claimed that the Linux RNG was not robust. However, those claims are based on two flawed assumptions. First, the authors assumed that Linux uses the event’s data as source of entropy and measures the jiffies to estimate the entropy amount, which indeed would have been wrong because the two are uncorrelated, whereas Linux assumes the entropy comes from the jiffies, and the event’s data is estimated to be of 0 entropy, which is sound. The second claim assumes that the attacker obtained the knowledge of the inner state of the generator and is able to control the refresh data (the source of randomness inserted into the generator). Obviously, in this case an attacker can maintain the knowledge of the inner state of the generator over time. That is why the robustness properties state that the attacker can either know the state at one point in time or control the refresh data, but never both at the same time. Thus, those claims of flaws in the Linux generator in version 3.7.8 were unfounded.
According to the first study and the changes made in the kernel version 4.8, the output of the non-blocking /dev/urandom or getrandom() should be used whenever possible and the output of /dev/random used only for backward compatibility reasons. The blocking behavior of /dev/random when not enough entropy has been estimated should not be relied upon in theory, because any measurement of entropy is inherently flawed.
To summarize, assuming that the Linux PRNG is well initialized with random data, it should be considered cryptographically secure, with the strongest security margin when using the output from getrandom() when called without flags.
Known attacks on the Linux RNG
According to the BSI study, the following attack scenarios can be conceived:
- Gutterman et al.:
- DoS by continuous calls to the
blocking_pool. - In the past (kernel version 4.8 and less), continuous read to
/dev/urandom(unblocking) could reduce the entropy ofinput_poolfaster than it was refreshed. This has been mitigated by using a stream cipher (Chacha20). - In the case of a system without storage (such as live CDs), the pools cannot be initialized at boot with their previous state. This has been mitigated by injecting 4 times 64 bits from
fast_pools intocrng_stateas soon as possible. Moreover, the syscallget_random()is blocking by default until the CRNG is initialized, preventing the issue when this syscall is used.
- DoS by continuous calls to the
- Lacharme:
- In previous version, when no entropy was collected at boot, the
input_poolandblocking_poolcould not produce new values./dev/urandombecame then a DRNG using a LFSR as a state transition. Before kernel version 3.13, the period of the LFSR was not optimal because the used polynomials were not irreducible. Since then, the polynomials have been fixed. And since kernel version 4.8, the use of a stream cipher completely solved the issue. - Their study concludes that the RNG is secure enough.
- In previous version, when no entropy was collected at boot, the
Dubious points
In pathological cases, /dev/urandom can output data that is not random enough and compromise the network protocols using it. This can be the case when the system just booted for the first time or when booted from a snapshot. Indeed, the kernel might not have had enough time to gather enough events to refresh the pools’ state. On a desktop system this issue should not arise, except for the first boot. See section Pools initialization. The problem remains in:
- embedded systems without writable non-volatile memory;
- cloned VMs, whose pools need to be refreshed before fetching random data.
The model used by the kernel to estimate the amount of entropy can be disputed [5][6], The estimation is not based on the content of the events but on their timing, yet the hardware can impact the time when events are received by the kernel and the sampling frequency could prevent the estimation to go under some threshold, thus preventing the pools to block when they should.
Noteworthy updates between versions 4.8 and 5.4
Version 4.8 introduced the used of the stream cipher Chacha20.
Only few updates of the code source were made between version 4.8 and 4.17 of the kernel. The updates are minor and do not affect the functional behavior of the generator.
From the version 4.17:
crng_stateis considered fully initialized when it receives 128 bits of entropy. Before, only 256 interrupts were enough.- Warnings are logged when random bytes are generated when the RNG is not fully initialized.
References
- Source code: github.com/torvalds/linux/blob/master/drivers/char/random.c (last version)
- Analysis of Random Number Generation in Virtual Environments, by the BSI, 2016.
- Documentation and Analysis of the Linux Random Number Generator, by the BSI, updated in 2019.
- Initialization of the CSPRNG by
crng_fast_load(), by forest, on security.stackexchange.com, 2018. - A model and Architecture for Pseudo-Random Generation and Applications to
/dev/random, by Boaz Barak and Shai Halevi, in ACM CCS 2005, DOI: 10.1145/1102120.1102148, 2005. - Security Analysis of Pseudo-Random Number Generators with Input:
/dev/randomis not Robust, by Yevgeniy Dodis, David Pointcheval, Sylvain Ruhault, Damien Vergnaud and Daniel Wichs, in ACM CCS 2013, DOI: 10.1145/2508859.2516653, 2013.









